矩阵变换，一句标准矩阵表示的变换
复合变换按照指定顺序将多个变换复合为一个变换
组合变换按照固定顺序组合一系列变换
表示二维 x-y 平面使用 3x3 矩阵进行自定义变换，上一篇文章中的四个变换类都是基于此得到，MtrixTransForm类是通过矩阵算法运行得到相应的效果
矩阵中第三列的值是固定不变的！ 原理： 原坐标（x0，y0）通过这个3*3矩阵
得到变换之后的新坐标（x1，y1）的过程如下： [x0,y0] *
，通过矩阵乘法可得到坐标 (x0 * M11+x0 * M21,y0 * M12+y0 * M22)之后，再加上 (OffsetX,OffsetY) 即可得到新坐标（x1，y1）。也即是说最终坐标 (x1,y1) : x1 = x0 * M11 + x0 * M21 + OffsetX , y1 = y0 * M12 + y0 * M22 + OffsetY.
1 <!--源码用法-->
2 3 <MatrixTransform Matrix=
" M11 M12 M21 M22 OffsetX OffsetY "></MatrixTransform>
示例：
<Grid x:Name=
" ContentPanel " Grid.Row=
" 1 " Margin=
" 12,0,12,0 ">
<!--<TextBlock x:Name=
" tb1 " FontSize=
" 72 " HorizontalAlignment=
" Center " VerticalAlignment=
" Center " Text=
" 变换文字示例 " Foreground=
" Cyan "></TextBlock>-->
<TextBlock x:Name=
" tbShow " FontSize=
" 72 " VerticalAlignment=
" Center " HorizontalAlignment=
" Center " Text=
" 变换文字示例 " Foreground=
" Cyan ">
<TextBlock.RenderTransform>
<MatrixTransform Matrix=
" 0,1,2,1,2,2 "></MatrixTransform>
</TextBlock.RenderTransform>
</TextBlock>
</Grid>
效果：
总结规律得到
m11 ——X轴缩放
m12 ——Y轴上倾斜
m21 ——X轴上倾斜
m22——Y轴缩放
offsetX ——X轴上的位移
offsetY ——Y轴上的位移
部分参考：http://www.cnblogs.com/crazypig/archive/2012/02/20/2359599.html
http://www.oschina.net/question/213217_49488
表示对变换效果的一种复合，在TransformGroup中可以包含其他的变换，当然也嵌套TransformGroup
代码：
<!--ContentPanel - TransformGroup-->
<Grid x:Name=
" ContentPanel " Grid.Row=
" 1 " Margin=
" 12,0,12,0 ">
<TextBlock x:Name=
" tbShow " FontSize=
" 72 " VerticalAlignment=
" Center " HorizontalAlignment=
" Center " Text=
" 变换文字示例 " Foreground=
" Cyan ">
<TextBlock.RenderTransform>
<TransformGroup>
<TranslateTransform X=
" -2 " Y=
" 3 "></TranslateTransform>
<ScaleTransform ScaleX=
" 0.8 " ScaleY=
" 0.9 "></ScaleTransform>
<RotateTransform Angle=
" 23 "></RotateTransform>
<TransformGroup>
<MatrixTransform Matrix=
" 1,0,1,1,0,1 "></MatrixTransform>
</TransformGroup>
</TransformGroup>
</TextBlock.RenderTransform>
</TextBlock>
</Grid>
这里需要注意的是我们在定义变换的顺序，因为每个变换都是基于上一个变换的基础进行变换，效果：
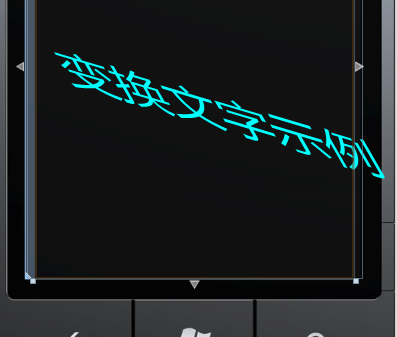
是表示对变换的一种组合，并且具有顺序性，所有的变换都是通过属性进行设置的
<!--ContentPanel - CompositeTransform-->
<Grid x:Name=
" ContentPanel " Grid.Row=
" 1 " Margin=
" 12,0,12,0 ">
<TextBlock x:Name=
" tbShow " FontSize=
" 72 " VerticalAlignment=
" Center " HorizontalAlignment=
" Center " Text=
" 变换文字示例 " Foreground=
" Cyan ">
<TextBlock.RenderTransform>
<CompositeTransform Rotation=
" 23 " TranslateX=
" -2 " TranslateY=
" 3 " ScaleX=
" 0.8 " ScaleY=
" 0.9 " ></CompositeTransform>
</TextBlock.RenderTransform>
</TextBlock>
</Grid>
上面代码中用到属性的意思Rotation表示旋转的角度，TranslateX表示在X轴平移的位置量，TranslateY表示在Y轴平移的位置量，ScaleX表示在X轴缩放的尺寸，ScaleY表示在Y轴缩放的尺寸；
TransformGroup 和CompositeTransfom异同：两者可以设置相同的属性得到相同的效果，在TransformGroup中我们可以使用 TransformGroup进行相同变换的多次使用，但是在CompositeTransfom中使用属性是不允许的，还有就是在 TransformGroup我们可以使用自定义变换，但是在组合变换CompositeTransfom中并没有该属性；两者还需要注意的是顺序性，不同的顺序，实现的效果不同；
本文转自shenzhoulong 51CTO博客，原文链接：http://blog.51cto.com/shenzhoulong/840745，如需转载请自行联系原作者